Hey math explorers! 👋
Are you struggling to figure out how to multiply fractions without getting confused by all the numbers and rules? Don’t worry — you’re definitely not alone.
Many students, parents, and even adults find fractions tricky. But once you learn the right method, multiplying fractions becomes super simple and logical.
In this article, we’ll cover:
- What multiplying fractions really means
- Step-by-step instructions (with easy examples)
- How to multiply mixed numbers
- Tips to simplify faster
- Practice problems and real-life uses
By the end, you’ll feel confident solving any fraction multiplication question that comes your way. Let’s get started! 🚀
🧩 What Does Multiplying Fractions Mean?
Before jumping into numbers, let’s understand the concept.
When you multiply fractions, you’re basically finding a part of a part.
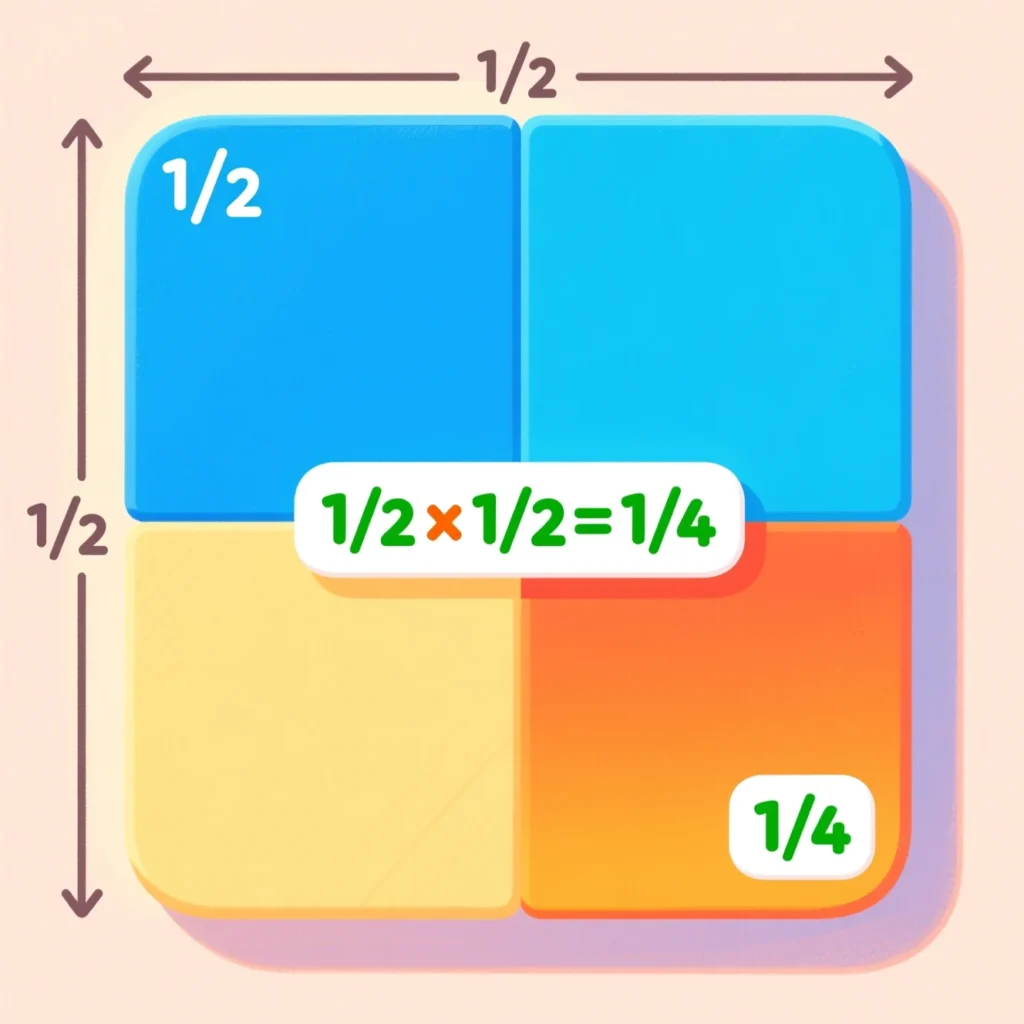
Example:
“What is ½ of ½?”
Visually, imagine a square divided into 2 equal parts (½). Now take half of that half — you get ¼ of the full square.
So:
½ × ½ = ¼
In simple words, multiplying fractions makes smaller parts because you’re taking a portion of another portion.
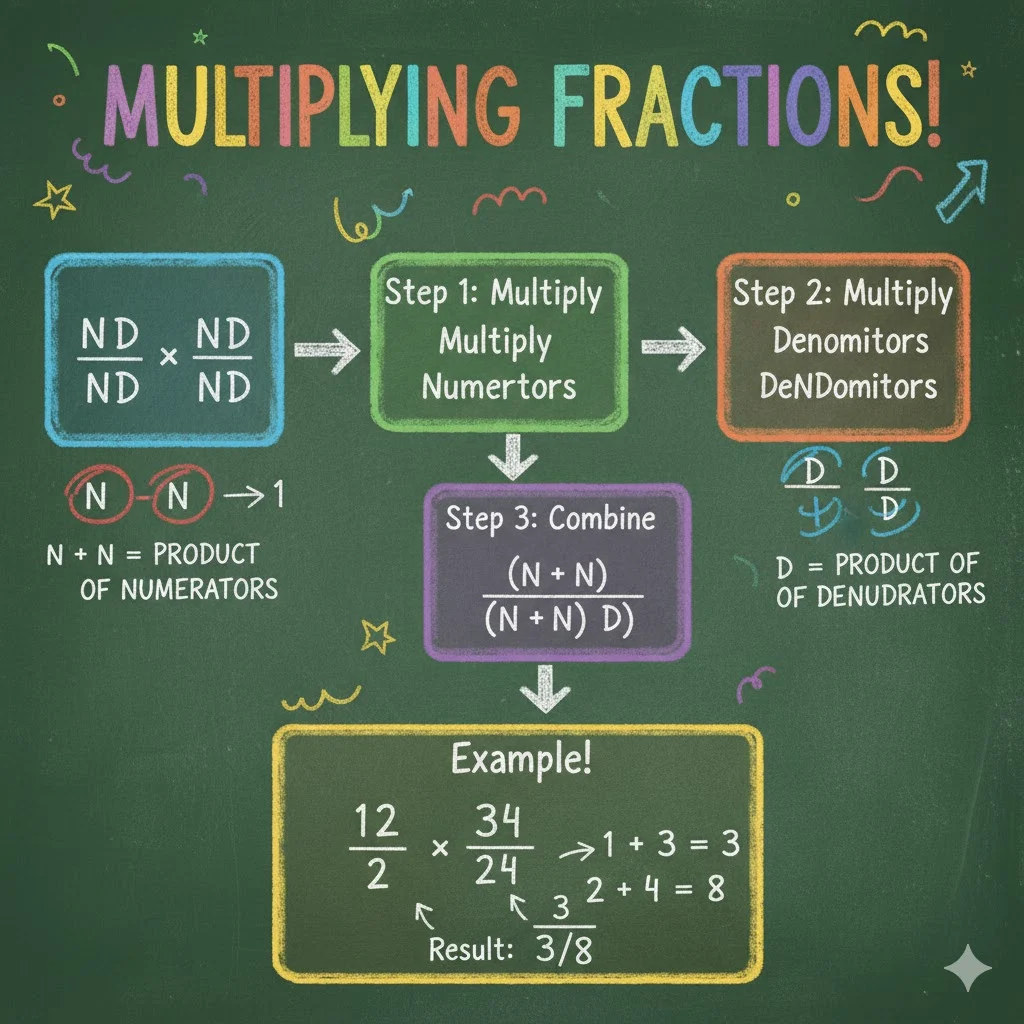
🔢 Step-by-Step Guide: How to Multiply Fractions
Here’s the easiest rule in math:
👉 Multiply the numerators (top numbers) and multiply the denominators (bottom numbers).
Step 1: Multiply the Numerators
Example:
2/3 × 4/5
Multiply the top numbers: 2 × 4 = 8
Step 2: Multiply the Denominators
3 × 5 = 15
Step 3: Write the New Fraction
8/15 ✅
That’s it! No need to find a common denominator or anything complicated.

🧮 Example 2: Multiplying Mixed Numbers
Mixed numbers are a mix of whole numbers and fractions (like 1½ or 2¾). To multiply them, first convert each to improper fractions.
Example:
1½ × 2¾
Convert to improper fractions:
1½ = 3/2
2¾ = 11/4
Now multiply:
(3/2) × (11/4) = 33/8
Convert back to a mixed number:
33 ÷ 8 = 4 R1 → 4⅛
✅ Final Answer: 4⅛

💡 Simplify Before You Multiply (Smart Trick)
You can save time by canceling common factors before multiplying.
Example:
3/4 × 8/9
8 and 4 share a common factor (4). Divide both by 4:
8 ÷ 4 = 2
4 ÷ 4 = 1
Now the problem becomes:
(3/1) × (2/9) = 6/9 = 2/3
✅ Final Answer: 2/3

🧠 Why Fraction Multiplication Works
Fractions represent parts of a whole. When you multiply them, you’re scaling one fraction by another. Think of it like zooming in — each multiplication reduces the size because you’re taking a part of a part.
For instance:
½ × ½ = ¼ (a smaller piece)
½ × 2 = 1 (you double it!)
So, multiplying fractions helps us represent portions in everyday life — from recipes to area calculations.
🍕 Real-Life Examples of Multiplying Fractions
- Cooking: A recipe needs ¾ cup of sugar, but you’re making half the recipe. → ½ × ¾ = ⅜ cup of sugar.
- Carpentry: A wooden board is ⅔ meter long. You need ¾ of that piece. → ¾ × ⅔ = ½ meter.
- School Projects: If ⅔ of a class likes sports, and ½ of those play football, then ⅓ of the class plays football. → ½ × ⅔ = ⅓.
✍️ Practice Problems
- ½ × ⅓ = ?
- ¾ × ⅖ = ?
- 2½ × ⅔ = ?
- ⅗ × ⅗ = ?
- 3⅓ × ¼ = ?
✅ Answers:
1. 1/6
2. 6/20 = 3/10
3. 5/3 = 1⅔
4. 9/25
5. 10/12 = 5/6
🧩 Common Mistakes to Avoid
- ❌ Adding instead of multiplying → Remember: ½ × ½ ≠ 1, it’s ¼!
- ❌ Forgetting to simplify → Always reduce fractions to simplest form.
- ❌ Skipping conversion for mixed numbers → Always convert to improper fractions first.
📘 Quick Recap
To Multiply Fractions:
- Multiply the top numbers (numerators)
- Multiply the bottom numbers (denominators)
- Simplify the result
Example:
(5/6) × (3/4) = 15/24 = 5/8
❓ Frequently Asked Questions (FAQs)
1. What’s the formula for multiplying fractions?
The formula is simple:
(a/b) × (c/d) = (a × c) / (b × d)
2. Do you need a common denominator to multiply fractions?
No. That’s only for addition or subtraction. Multiplication doesn’t need a common denominator.
3. What happens when you multiply by a whole number?
Turn the whole number into a fraction (e.g., 5 = 5/1) and multiply normally.
(2/3) × 5 = 10/3 = 3⅓
4. Is multiplying fractions always smaller?
Usually yes — unless one of the fractions is greater than 1.
5. How to check if your answer is correct?
Estimate! If you multiply two small fractions like ½ × ⅓, your answer should be smaller than both — that’s 1/6.
🏁 Final Thoughts
Multiplying fractions doesn’t have to be scary — it’s just multiply across and simplify. Once you practice a few examples, it’ll feel natural.
Whether you’re baking, building, or solving math homework, fractions help you deal with real-life “parts of parts.”
So next time someone asks, “Hey, how do you multiply fractions?”, you’ll be the one explaining it like a pro. 💪