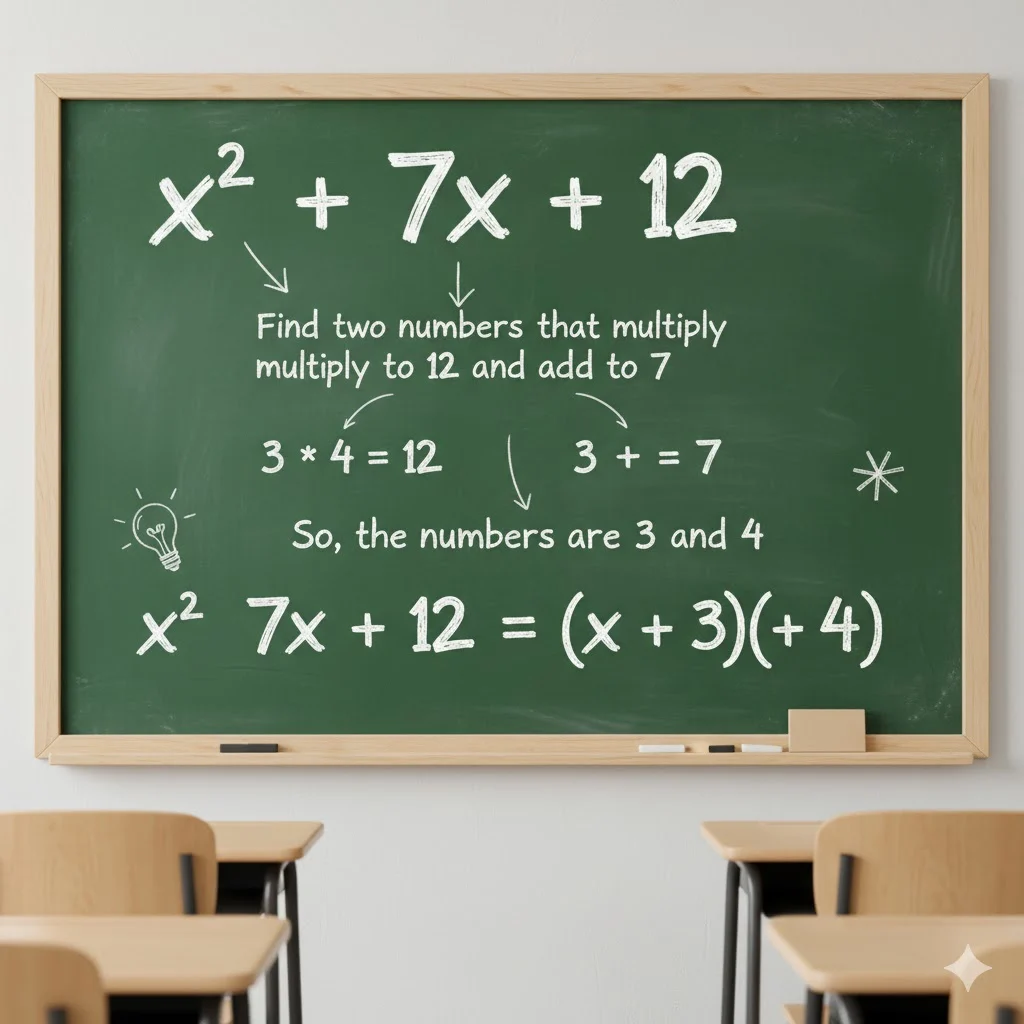Hey math learner 👋 — if you’ve ever stared at an equation like x² + 7x + 12 and thought, “What do I even do with this?” — this guide is for you!
Factoring is one of the most foundational algebra skills. It helps you simplify equations, solve quadratic problems, and understand how numbers really work together.
This article will teach you:
- ✅ What factoring means (in simple terms)
- ✅ How to factor numbers, trinomials, and polynomials
- ✅ Common patterns and shortcuts
- ✅ Real-life examples + practice questions
By the end, you’ll not only understand factoring — you’ll be confident solving any factoring problem that comes your way.
🧩 What Does “Factoring” Mean in Math?
Factoring means breaking a number or expression into smaller parts (factors) that multiply together to create the original value.
It’s the opposite of multiplying. When you multiply, you combine smaller numbers to get a bigger one. When you factor, you take a big number (or expression) and find what smaller numbers multiply to make it.
💬 Example 1 (Numbers)
12 = 3 × 4 → 3 and 4 are factors of 12.
💬 Example 2 (Algebra)
x² + 5x + 6 = (x + 2)(x + 3) → (x + 2) and (x + 3) are factors of the expression.
🔢 How to Factor Numbers (Step-by-Step)
Step 1: Find All Factor Pairs
Write down every pair of numbers that multiply to give the target number.
Example: 24
1 × 24
2 × 12
3 × 8
4 × 6
✅ So the factors of 24 are: 1, 2, 3, 4, 6, 8, 12, 24.
Step 2: Use Prime Factorization
Prime factorization breaks a number into only prime numbers.
Example: 24
24 ÷ 2 = 12 → 12 ÷ 2 = 6 → 6 ÷ 2 = 3 → 3 ÷ 3 = 1
✅ Prime Factorization: 2 × 2 × 2 × 3 → 2³ × 3
🧠 Why It Matters: It helps simplify fractions, find GCF, and build a base for algebraic factoring.
🧮 How to Factor Algebraic Expressions
Factoring algebraic expressions helps you simplify or solve equations. Let’s explore all the key methods.
1. Factoring Out the GCF (Greatest Common Factor)
Example: 6x² + 9x → 3x(2x + 3)
✅ Always do this first before any other method.
2. Factoring Trinomials (x² + bx + c)
Example: x² + 7x + 12 → (x + 3)(x + 4)
Because 3 × 4 = 12 and 3 + 4 = 7.
3. Factoring with a Leading Coefficient (ax² + bx + c)
Example: 2x² + 7x + 3
a × c = 6 → find two numbers that multiply to 6 and add to 7 (6 and 1).
Rewrite: 2x² + 6x + x + 3 → group → (2x² + 6x) + (x + 3)
✅ Factored Form: (2x + 1)(x + 3)
4. Factoring by Grouping (4 Terms)
Example: x³ + 3x² + 2x + 6 → (x³ + 3x²) + (2x + 6)
x²(x + 3) + 2(x + 3) → ✅ (x + 3)(x² + 2)
5. Difference of Squares
Formula: a² – b² = (a + b)(a – b)
Example: x² – 49 = (x + 7)(x – 7)
6. Perfect Square Trinomials
Example: x² + 6x + 9 = (x + 3)²
7. Sum and Difference of Cubes
Formulas:
a³ + b³ = (a + b)(a² – ab + b²)
a³ – b³ = (a – b)(a² + ab + b²)
Example: x³ + 8 = (x + 2)(x² – 2x + 4)
🧠 Common Factoring Patterns (Cheat Sheet)
| Pattern Type | Formula | Example | Factored Form |
|---|---|---|---|
| GCF | a(b + c) | 3x² + 6x | 3x(x + 2) |
| Trinomial | x² + bx + c | x² + 5x + 6 | (x + 2)(x + 3) |
| a ≠ 1 | ax² + bx + c | 2x² + 7x + 3 | (2x + 1)(x + 3) |
| Grouping | 4 Terms | x³ + 3x² + 2x + 6 | (x + 3)(x² + 2) |
| Difference of Squares | a² – b² | x² – 16 | (x + 4)(x – 4) |
| Perfect Square | a² + 2ab + b² | x² + 6x + 9 | (x + 3)² |
| Sum of Cubes | a³ + b³ | x³ + 8 | (x + 2)(x² – 2x + 4) |
💡 Pro Tips for Factoring Like a Pro
- Always check for a GCF first.
- Watch for negative signs. A small mistake changes everything.
- Rewrite or group terms if stuck.
- Spot perfect squares and cubes quickly.
- Verify by expanding to confirm your result.
🧩 Practice Problems
Try these yourself 👇 (Factor completely)
- 15x² + 20x
- x² + 9x + 20
- 3x² + 8x + 4
- x³ – 27
- 2x² – 18
✅ Answers:
1. 5x(3x + 4)
2. (x + 4)(x + 5)
3. (3x + 2)(x + 2)
4. (x – 3)(x² + 3x + 9)
5. 2(x² – 9) = 2(x + 3)(x – 3)
❓ Frequently Asked Questions (FAQ)
What is factoring used for in real life?
Factoring helps in engineering, finance, and coding — anywhere large problems need to be broken into smaller, manageable parts.
What is the easiest way to factor in algebra?
Start by taking out the Greatest Common Factor (GCF) and then look for patterns like trinomials or difference of squares.
How do you know when something can’t be factored?
If there are no real numbers that fit the pattern (like x² + 4), it’s called a prime expression.
Why is factoring important in quadratic equations?
It helps find the x-intercepts or roots. Example: x² + 5x + 6 = 0 → (x + 2)(x + 3) = 0 → x = -2, -3.
🌟 Final Thoughts: Master Factoring for Life
Factoring isn’t just an algebra trick — it’s mathematical thinking. It trains your brain to see patterns, simplify problems, and connect relationships between numbers.
If you practice just 10–15 minutes a day, you’ll soon factor any expression like a pro.
💬 Did this guide help you understand how to factor? Share your thoughts or math questions below — I’d love to help!