How to Divide Fractions Easily | Keep, Change, Flip Rule Explained with Examples

Hey there, math explorer! 👋

If you’ve ever wondered “How do I divide fractions?” or found yourself confused by tiny numbers stacked on each other — you’re not alone.

Dividing fractions seems tricky, but once you understand the Keep, Change, Flip rule, it’s as easy as pie 🥧. Whether you’re a student, teacher, or parent helping with homework, this post will help you finally get it.

Here’s what we’ll cover:

• What dividing fractions really means
• The logic behind the process
• The “Keep, Change, Flip” shortcut
• Step-by-step examples
• Dividing mixed numbers
• Common mistakes and real-life applications
• FAQs and practice problems

---

🧩 What Does Dividing Fractions Mean?

Dividing fractions tells you how many times one fraction fits into another.

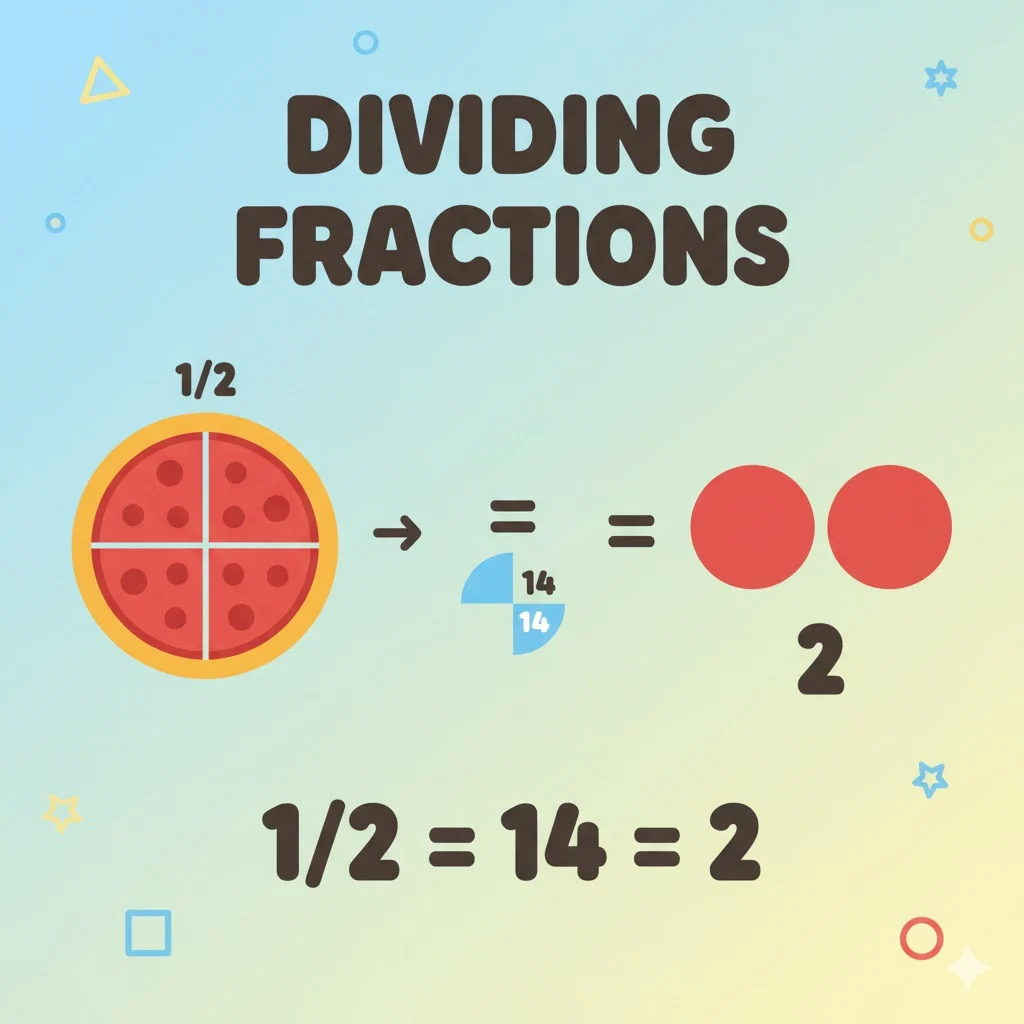
Think about it like this:
½ ÷ ¼ = ?

You’re asking, “How many one-fourths are in one-half?”

Visually, a ½ slice of pizza can fit two ¼ slices inside it — so the answer is 2.

½ ÷ ¼ = 2

That’s why when dividing by a small fraction, the result is often larger, not smaller — because you’re finding how many smaller parts fit inside a given piece.

---

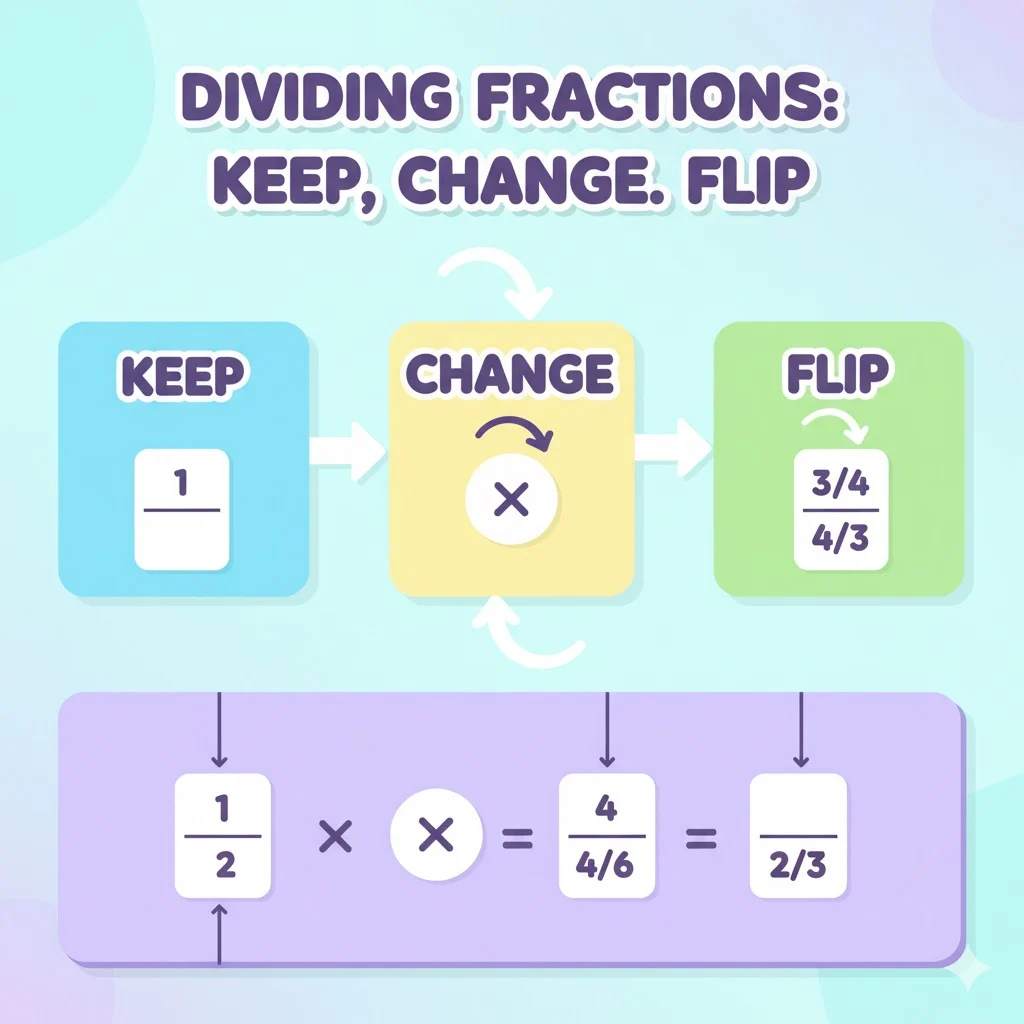
🔢 The Simple Trick: Keep, Change, Flip

This is the golden rule for dividing fractions — the one math teachers love:

KEEP – CHANGE – FLIP

Here’s what it means:

1. Keep the first fraction as it is.
2. Change the division sign (÷) to multiplication (×).
3. Flip the second fraction upside down (find its reciprocal).

Now, just multiply like normal. That’s it! 🎯

---

🧮 Step-by-Step Example

Example 1:
2/3 ÷ 4/5

Step 1: Keep the first fraction → 2/3
Step 2: Change ÷ to ×
Step 3: Flip the second fraction → 5/4

Now multiply:
2/3 × 5/4 = 10/12
Simplify 10/12 → 5/6

✅ Final Answer: 5/6

---

🧠 Why Does “Keep, Change, Flip” Work?

At first, it might feel like magic — but there’s solid math logic behind it.

Division means: “How many 4/5s are in 2/3?”

To find that, we convert the question into a multiplication problem that’s easier to solve:

2/3 ÷ 4/5 = 2/3 × 5/4

By flipping 4/5 to 5/4, we find the reciprocal — the value that, when multiplied, equals 1.

In short, dividing by a fraction is the same as multiplying by its reciprocal.

---

🧮 Example 2: Dividing Mixed Numbers

1½ ÷ ¾

Step 1: Convert mixed numbers to improper fractions.
1½ = 3/2

Step 2: Keep, Change, Flip
3/2 ÷ 3/4 = 3/2 × 4/3

Step 3: Multiply
3 × 4 = 12
2 × 3 = 6
12/6 = 2

✅ Final Answer: 2

---

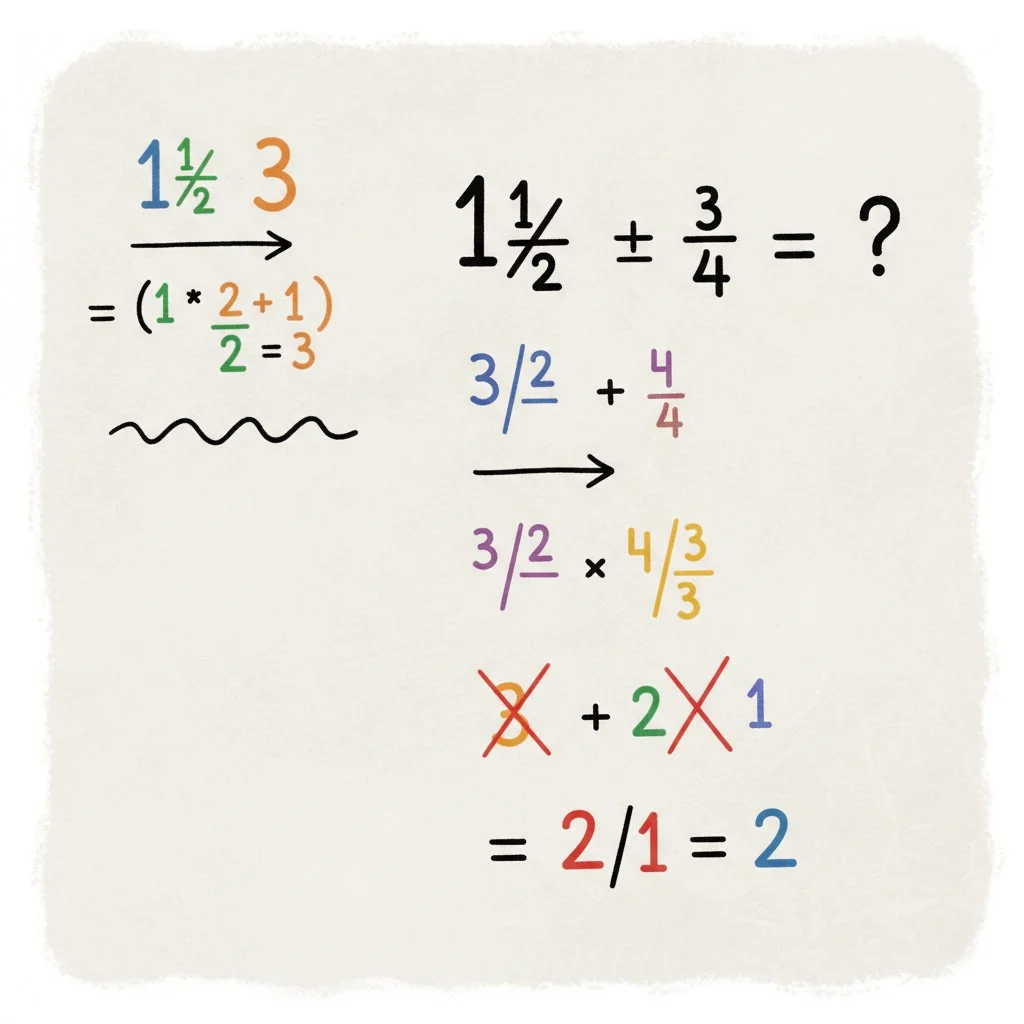
💡 Simplify Before You Multiply

Simplifying before multiplying makes your math cleaner and faster.

Example:
4/5 ÷ 2/3
→ Keep, Change, Flip → 4/5 × 3/2

Now simplify:
4 ÷ 2 = 2 → 2/5 × 3/1 = 6/5 = 1⅕

✅ Final Answer: 1⅕

---

🔍 Real-Life Examples of Dividing Fractions

1. Cooking 🍪

You have ¾ cup of sugar and each cookie batch needs ¼ cup.
¾ ÷ ¼ = 3
✅ You can make 3 batches.

2. Measuring Wood 🪵

You have a 2-meter plank and want pieces of ½ meter.
2 ÷ ½ = 4
✅ You can cut 4 equal pieces.

3. Sharing Drinks 🥤

You have ⅔ of a bottle, and each glass takes ⅙ of a bottle.
⅔ ÷ ⅙ = 4
✅ You can pour 4 glasses.

---

✍️ Practice Problems

1. ½ ÷ ⅓ = ?
2. ¾ ÷ ⅙ = ?
3. ⅖ ÷ ⅘ = ?
4. 2⅔ ÷ ⅔ = ?
5. 1½ ÷ ¼ = ?

Answers:
1. ½ × 3/1 = 3/2 = 1½
2. ¾ × 6/1 = 18/4 = 4½
3. ⅖ × 5/4 = 20/20 = 1
4. 8/3 × 3/2 = 24/6 = 4
5. 3/2 × 4/1 = 12/2 = 6

---

⚠️ Common Mistakes Students Make

• ❌ Forgetting to flip the second fraction.
• ❌ Dividing numerators and denominators directly.
• ❌ Not simplifying the final answer.

✔ Always simplify and double-check your steps!

---

📘 Quick Recap

Steps to Divide Fractions:

1. Keep the first fraction.
2. Change ÷ to ×.
3. Flip the second fraction.
4. Multiply across.
5. Simplify.

Example:
5/8 ÷ 3/4 = 5/8 × 4/3 = 20/24 = 5/6
✅ Final Answer: 5/6

---

❓ Frequently Asked Questions (FAQs)

1. What’s the easiest way to divide fractions?

Use the Keep, Change, Flip method — it’s simple and foolproof.

2. Why do we flip the second fraction?

Because dividing by a fraction is the same as multiplying by its reciprocal.

3. What if one number is a whole number?

Turn it into a fraction (e.g., 5 = 5/1) and follow the same steps.

4. Should I always simplify my answer?

Yes, always simplify for neat and accurate results.

---

🏁 Final Thoughts

Dividing fractions isn’t hard — it’s just a pattern. Once you remember Keep, Change, Flip, you’ll never get confused again!

Dividing fractions isn’t about making numbers smaller — it’s about finding how many times one piece fits into another.

So next time you see a problem like ⅔ ÷ ⅖, smile and say:
“Easy! Keep, Change, Flip — and done!” 💪